[BOJ] 볼 모으기 17615번 C++

문제

빨간색 볼과 파란색 볼이 <그림 1>에서 보인 것처럼 일직선상에 섞여 놓여 있을 때, 볼을 옮겨서 같은 색 볼끼리 인접하게 놓이도록 하려고 한다. 볼을 옮기는 규칙은 다음과 같다.

1. 바로 옆에 다른 색깔의 볼이 있으면 그 볼을 모두 뛰어 넘어 옮길 수 있다. 즉, 빨간색 볼은 옆에 있는 파란색 볼 무더기를 한 번에 뛰어 넘어 옮길 수 있다. 유사하게, 파란색 볼은 옆에 있는 빨간색 볼 무더기를 한 번에 뛰어 넘어 옮길 수 있다.
2. 옮길 수 있는 볼의 색깔은 한 가지이다. 즉, 빨간색 볼을 처음에 옮겼으면 다음에도 빨간색 볼만 옮길 수 있다. 유사하게, 파란색 볼을 처음에 옮겼으면 다음에도 파란색 볼만 옮길 수 있다.

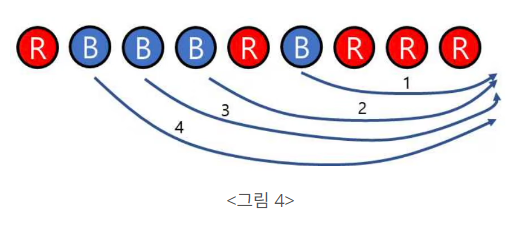
예를 들어, 처음에 볼이 <그림 1>에서 보인 것처럼 있을 때, 빨간 볼을 <그림 2>에서 보인 것처럼 옮긴 후, <그림 3>에서 보인 것처럼 옮긴다면 두 번 만에 같은 색끼리 모을 수 있다.

 

반면에 파란색 볼을 선택하여 에서 보인 것처럼 옮기면(화살표에 있는 수는 옮기는 순서를 나타낸다) 네 번을 옮겨야 같은 색의 볼끼리 모을 수 있다.

 

일직선상에 놓여 있는 볼에 관한 정보가 주어질 때, 규칙에 따라 볼을 이동하여 같은 색끼리 모으되 최소 이동횟수를 찾는 프로그램을 작성하시오.

입력

첫 번째 줄에는 볼의 총 개수 N이 주어진다. (1 ≤ N ≤ 500,000) 다음 줄에는 볼의 색깔을 나타내는 문자 R(빨간색 볼) 또는 B(파란색 볼)가 공백 없이 주어진다. 문자열에는 R 또는 B 중 한 종류만 주어질 수도 있으며, 이 경우 답은 0이 된다.

출력

최소 이동횟수를 출력한다.

서브태스크

번호배점제한

1	15	N ≤ 10
2	22	N ≤ 1,000
3	14	N ≤ 500,000, 처음 상태에서 모든 파란 공은 연속해서 존재한다.
4	49	원래의 제약조건 이외에 아무 제약조건이 없다.

 

접근 방식

 

생각보다 풀이를 떠올리기 쉽지 않았던 문제였다..

구현은 생각보다 간단하다

빨간볼, 파란볼에 대해 총 4가지 경우를 모두 계산해 최소값을 구하면된다.

1. 빨간볼을 왼쪽으로 모는 경우

2. 파란볼을 왼쪽으로 모는 경우

3. 빨간볼을 오른쪽으로 모는 경우

4. 파란볼을 오른쪽으로 모는 경우

 

이를 위해 각 경우에서의 이동 횟수를 계산하면 된다.

예를 들어, 빨간볼을 모두 왼쪽으로 모으려면, 왼쪽에서 연속된 빨간색 구간은 그래도 두고, 그 뒤에 나오는 모든 빨간색을 이동시켜야 한다.

따라서, 왼쪽에 연속된 빨간볼의 개수를 모두 구하고

전체 빨간볼의 개수에서 왼쪽에 연속된 빨간볼의 개수(이동하지 않아도 되는 빨간볼의 개수) 를 빼면된다.

 

즉, 모든 경우에 대해 위의 방식으로 이동 횟수를 구한 뒤, 가장 최소값을 구하면된다.

 

 

코드

 

#include<bits/stdc++.h>
using namespace std;

int main() {
    int n;cin>>n;
    string str; cin>>str;

    int leftR = 0, leftB = 0, rightR = 0, rightB = 0;

    for(int i=0; i<n; i++) {
        if(str[i] == 'R') leftR++;
        else break;
    }

     for(int i=0; i<n; i++) {
        if(str[i] == 'B') leftB++;
        else break;
    }

    for(int i=n-1; i>=0; i--) {
        if(str[i] == 'R') rightR++;
        else break;
    }

    for(int i=n-1; i>=0; i--) {
        if(str[i] == 'B') rightB++;
        else break;
    }

    int totalR = count(str.begin(), str.end(), 'R');
    int totalB = count(str.begin(), str.end(), 'B');

    int result = min({totalR - leftR, totalB - leftB, totalR - rightR, totalB - rightB});

    cout<<result;



    
}