[BOJ] 다리 놓기 1010번 C++

문제
재원이는 한 도시의 시장이 되었다. 이 도시에는 도시를 동쪽과 서쪽으로 나누는 큰 일직선 모양의 강이 흐르고 있다. 하지만 재원이는 다리가 없어서 시민들이 강을 건너는데 큰 불편을 겪고 있음을 알고 다리를 짓기로 결심하였다. 강 주변에서 다리를 짓기에 적합한 곳을 사이트라고 한다. 재원이는 강 주변을 면밀히 조사해 본 결과 강의 서쪽에는 N개의 사이트가 있고 동쪽에는 M개의 사이트가 있다는 것을 알았다. (N ≤ M)
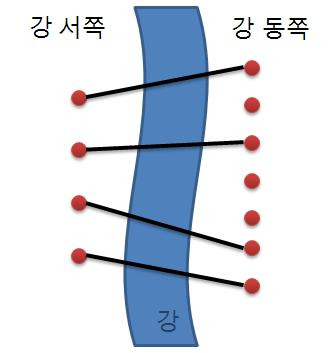
재원이는 서쪽의 사이트와 동쪽의 사이트를 다리로 연결하려고 한다. (이때 한 사이트에는 최대 한 개의 다리만 연결될 수 있다.) 재원이는 다리를 최대한 많이 지으려고 하기 때문에 서쪽의 사이트 개수만큼 (N개) 다리를 지으려고 한다. 다리끼리는 서로 겹쳐질 수 없다고 할 때 다리를 지을 수 있는 경우의 수를 구하는 프로그램을 작성하라.
입력
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.
출력
각 테스트 케이스에 대해 주어진 조건하에 다리를 지을 수 있는 경우의 수를 출력한다.
접근 방식
문제의 핵심은 서쪽 강의 n개의 지점을 동쪽 강의 m개의 지점 중에서 어떻게 선택하느냐다.
이는 즉, 조합을 이용해 구할 수 있고 mCn을 구하는 문제가 된다.
이때 조합 C(m,n을 구하기 위해서는)
C(m,n) = m! / n! * (m-n)!이고
이는 다음과 같은 DP 점화식을 이용해 풀 수 있다.
C(i,j) = C(i-1, j) (i번째 원소를 선택하지 않는 경우) + C(i-1, j-1) (i번째 원소를 선택하는 경우);
이를 코드로 구현하면 다음과 같이 풀 수 있당
코드
#include<bits/stdc++.h>
using namespace std;
long long dp[33][33];
int main() {
int T; cin>>T;
dp[0][0] = 1;
for(int i=1; i<=30; i++) {
dp[i][0] = 1;
for(int j=1; j<=30; j++) {
dp[i][j] = dp[i-1][j] + dp[i-1][j-1];
}
}
while(T--) {
int n,m; cin>>n>>m;
cout<<dp[m][n]<<'\n';
}
}