
문제
<그림 1>과 같이 정사각형 모양을 한 다섯 종류의 색종이가 있다. 색종이의 크기는 1×1, 2×2, 3×3, 4×4, 5×5로 총 다섯 종류가 있으며, 각 종류의 색종이는 5개씩 가지고 있다.
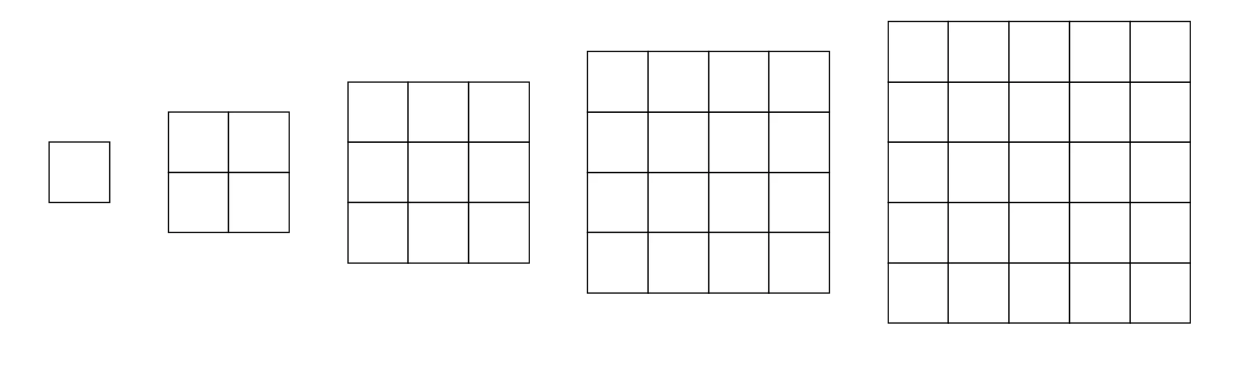
<그림 1>
색종이를 크기가 10×10인 종이 위에 붙이려고 한다. 종이는 1×1 크기의 칸으로 나누어져 있으며, 각각의 칸에는 0 또는 1이 적혀 있다. 1이 적힌 칸은 모두 색종이로 덮여져야 한다. 색종이를 붙일 때는 종이의 경계 밖으로 나가서는 안되고, 겹쳐도 안 된다. 또, 칸의 경계와 일치하게 붙여야 한다. 0이 적힌 칸에는 색종이가 있으면 안 된다.
종이가 주어졌을 때, 1이 적힌 모든 칸을 붙이는데 필요한 색종이의 최소 개수를 구해보자.
입력
총 10개의 줄에 종이의 각 칸에 적힌 수가 주어진다.
출력
모든 1을 덮는데 필요한 색종이의 최소 개수를 출력한다. 1을 모두 덮는 것이 불가능한 경우에는 -1을 출력한다.
접근 방식
먼저 백트래킹으로 가능한 모든 경우의 수를 탐색하고자 하였다
이를 위해 다음과 같은 과정을 거쳤다
1. 먼저 모든 칸을 탐색하면서 1인 부분을 찾고
2. 가능한 모든 크기의 색종이를 붙임
3. 붙일 수 있는 경우 모든 크기의 색종이를 다 사용한 경우는 되돌아가고
4. 색종이를 붙이는 과정에서 최소 개수를 갱신함
따라서 현재 색종이가 사용 가능하고
현재 칸에 해당 색종이를 붙일 수 있다면
붙이고 다음 탐색을 이어가고
돌아와서는 다시 색종이를 모두 떼어주는 코드를 작성했다
주의할 점은 현재 칸에 만약 5 x 5 크기의 색종이를 붙이고 싶은데
만약 현재 x,y위치에서 x+5, y+5한 값이 10X10을 넘어가는지 꼭 확인해주어야 한다!!!!
코드
#include<bits/stdc++.h>
using namespace std;
int mat[10][10], ans = 100;
int paper[6] = {0,5,5,5,5,5};
bool check(int x, int y, int n) {
if(x + n > 10 || y + n > 10) return false;
for(int i=x; i<x+n; i++) {
for(int j=y; j<y+n; j++) {
if(mat[i][j] == 0) return false;
}
}
return true;
}
void attach(int x, int y, int n , int value) {
for(int i = x; i < x + n; i++) {
for(int j = y; j < y + n; j++) {
mat[i][j] = value;
}
}
}
void sol(int x, int y, int cnt) {
if( y == 10 ) {
sol(x+1, 0, cnt);
return;
}
if( x == 10 ) {
ans = min(cnt, ans);
return;
}
if(mat[x][y] != 1) {
sol(x, y+1, cnt);
return;
}
for(int i=5; i>=1; i--) {
if(paper[i] > 0 && check(x, y, i)) {
attach(x,y,i,0);
paper[i]--;
sol(x,y+1, cnt+1);
paper[i]++;
attach(x,y,i,1);
}
}
}
int main() {
for(int i=0; i<10; i++) {
for(int j=0; j<10; j++) {
cin>>mat[i][j];
}
}
sol(0,0,0);
if(ans == 100) cout<<-1;
else cout<<ans;
}'Algorithm' 카테고리의 다른 글
| [BOJ] 비밀번호 13908번 C++ (0) | 2024.07.13 |
|---|---|
| [BOJ] 영재의 시험 19949번 C++ (0) | 2024.06.28 |
| [BOJ] 로마 숫자 만들기 16922번 C++ (0) | 2024.06.25 |
| [BOJ] 죽음의 비 22944번 C+ (0) | 2024.06.25 |
| [BOJ] 모든 순열 10974번 C++ (0) | 2024.06.22 |
