
문제
행의 수가 N이고 열의 수가 M인 격자의 각 칸에 1부터 N×M까지의 번호가 첫 행부터 시작하여 차례로 부여되어 있다. 격자의 어떤 칸은 ○ 표시가 되어 있다. (단, 1번 칸과 N × M번 칸은 ○ 표시가 되어 있지 않다. 또한, ○ 표시가 되어 있는 칸은 최대 한 개이다. 즉, ○ 표시가 된 칸이 없을 수도 있다.)
행의 수가 3이고 열의 수가 5인 격자에서 각 칸에 번호가 1부터 차례대로 부여된 예가 아래에 있다. 이 격자에서는 8번 칸에 ○ 표시가 되어 있다.
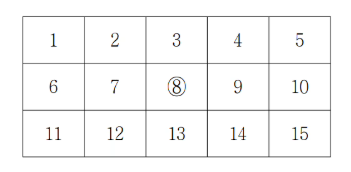
격자의 1번 칸에서 출발한 어떤 로봇이 아래의 두 조건을 만족하면서 N×M번 칸으로 가고자 한다.
- 조건 1: 로봇은 한 번에 오른쪽에 인접한 칸 또는 아래에 인접한 칸으로만 이동할 수 있다. (즉, 대각선 방향으로는 이동할 수 없다.)
- 조건 2: 격자에 ○로 표시된 칸이 있는 경우엔 로봇은 그 칸을 반드시 지나가야 한다.
위에서 보인 것과 같은 격자가 주어질 때, 로봇이 이동할 수 있는 서로 다른 경로의 두 가지 예가 아래에 있다.
- 1 → 2 → 3 → 8 → 9 → 10 → 15
- 1 → 2 → 3 → 8 → 13 → 14 → 15
격자에 관한 정보가 주어질 때 로봇이 앞에서 설명한 두 조건을 만족하면서 이동할 수 있는 서로 다른 경로가 총 몇 개나 되는지 찾는 프로그램을 작성하라.
입력
입력의 첫째 줄에는 격자의 행의 수와 열의 수를 나타내는 두 정수 N과 M(1 ≤ N, M ≤ 15), 그리고 ○로 표시된 칸의 번호를 나타내는 정수 K(K=0 또는 1 < K < N×M)가 차례로 주어지며, 각 값은 공백으로 구분된다. K의 값이 0인 경우도 있는데, 이는 ○로 표시된 칸이 없음을 의미한다. N과 M이 동시에 1인 경우는 없다.
출력
주어진 격자의 정보를 이용하여 설명한 조건을 만족하는 서로 다른 경로의 수를 계산하여 출력해야 한다.
접근 방법
먼저, 모든 좌표를 방문하면서 해당 칸으로 갈 수 있는 경우의 수를 모두 구한다
이는 dp 배열을 사용하면 간단하게 구할 수 있는데
로봇은 오른쪽에 인접한 칸, 아래에 인접한 칸으로만 이동할 수 있기때문에
dp[i][j] = dp[i-1][j] + dp[i][j-1] 으로 구할 수 있다
따라서 K가 0이라면 dp[N][M]을 출력하면 된다
하지만, K가 0이 아니라면
(1,1) => K숫자가 존재하는 좌표까지 경우의 수를 저장하고
dp 배열을 초기화시켜서
K숫자가 존재하는 좌표 => (N,M)까지의 경우의 수를 새롭게 구해준다
따라서 (1,1) => K까지의 경우의 수와 K => (N,M)까지의 경우의 수를 곱해주면 경우의 수를 구할 수 있다
코드
#include<bits/stdc++.h>
using namespace std;
int main() {
int N,M,K;
cin>>N>>M>>K;
vector<vector<int>> dp(N + 1, vector<int>(M + 1, 0));
dp[1][1] = 1;
for(int i=1; i<=N; i++) {
for(int j=1; j<=M; j++) {
if(i == 1 && j == 1) continue;
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
if(K > 0) {
int x = (K-1)/M + 1;
int y = (K-1)%M + 1;
int pathTo = dp[x][y];
dp = vector<vector<int>>(N+1, vector<int>(M+1, 0));
dp[x][y] = 1;
for(int i=x; i<=N;i++) {
for(int j=y; j<=M; j++) {
if(i == x && j == y) continue;
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
int pathFrom = dp[N][M];
cout<<pathTo * pathFrom;
}
else cout<<dp[N][M];
}'Algorithm' 카테고리의 다른 글
| [BOJ] 카드 구매하기 2 16194번 C++ (2) | 2025.02.14 |
|---|---|
| [BOJ] 회의실 배경 3 19622번 C++ (0) | 2025.02.11 |
| [BOJ] 징검다리 건너기 (small) 22869번 C++ (0) | 2025.01.19 |
| [BOJ] 쉬운 계단 수 10844번 C++ (0) | 2025.01.16 |
| [BOJ] 가장 긴 짝수 연속한 부분 수열 (small) 22857번 C++ (0) | 2025.01.14 |
